Dijkstra’s Algorithm In Swift
If you’ve ever heard of the term Graph Theory, surely you’re acquaintance with the Dijkstra’s Algorithm.
If you’re not, it’s all right! This article includes everything you need to know.
Quick Introduction
This chapter will bring you up to speed on what Graph Theory and the Dijkstra’s Algorithm are.
If you’re confident enough, you can skip this part! (🚀 jump to the Swift Time chapter)
Graph Theory

See the picture above? This is a what in Mathematics and Computer Science we call a Graph.
The circles are called Nodes (or vertices) and they represent the graph entities (more on this later) while the lines connecting the nodes are called Connections (or edges).
These connections, which always connect two nodes, are mainly of two types: bidirectional and mono-directional.
The former means that the connection works in both ways (duh!), while the latter means that the connection exists only from one node to the other, but not vice-versa (you will need a second connection to go the other way around).
These simple concepts have huge applications all over the world and you are probably using them all the time!
Real World Examples
Bidirectional Graph: Facebook
Let’s visualize your Facebook friends Graph!
You might end up with something like this:
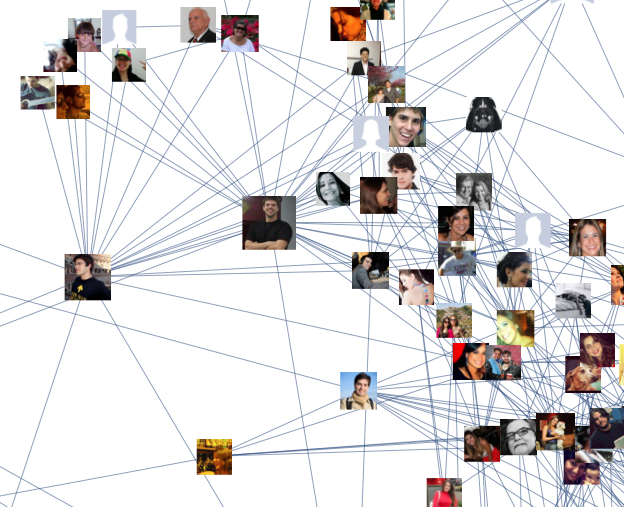
Picture from Mathematica StackExchange.
In this graph each node is a person, and each (bidirectional) connection represents the friendship between these people.
“Coincidentally” Facebook has a developer API called Graph.
Mono-directional Graph: Twitter
If we take a look at our followers on Twitter, the result might be something like this:
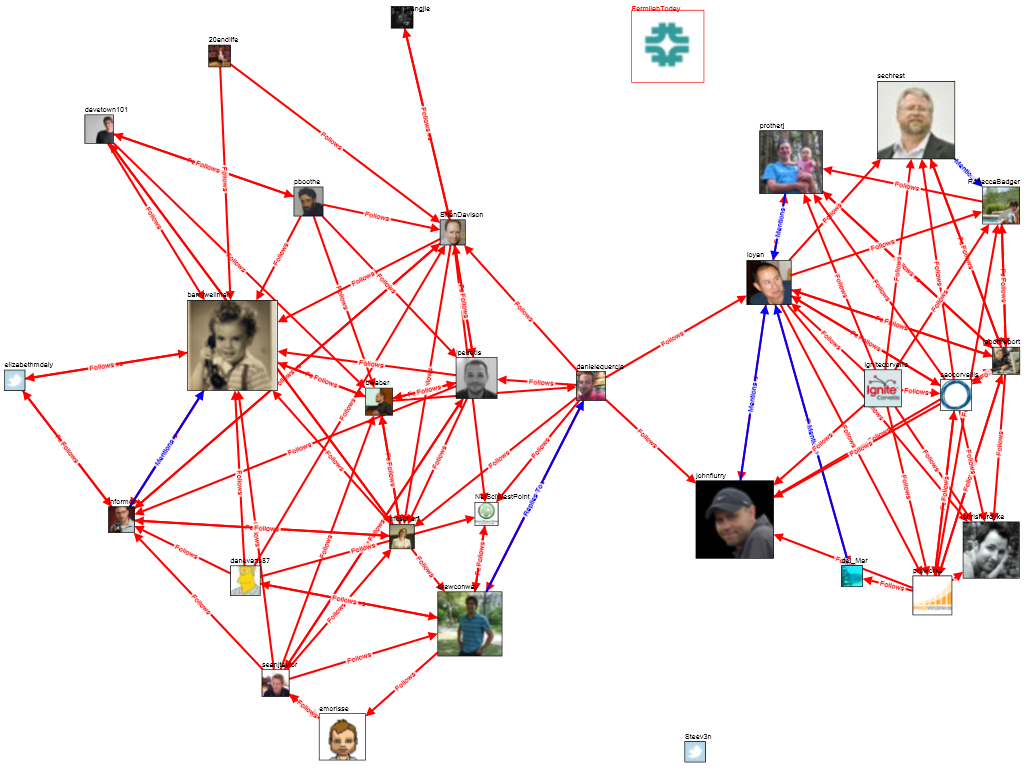
Picture from Social Media Research Foundation.
In this case each node is a Twitter Account, but the connections now are mono-directional, because if I follow you, this doesn’t imply that you are following me back.
Dijkstra’s Algorithm
Now that we understand what a Graph is, let’s talk about one of its hottest topics: the Shortest Path Problem.
This challenge is super simple to understand:
given two nodes in one Graph, find the shortest way to go from one node to the other (if it exists).
For us it’s a simple game (like solving a maze), but for a machine it’s a challenge that has to be solved as quick as possible.
Again, this is something that you’re using all the time, just think about how the Apple Maps App computes the best route, or how LinkedIn determines that a profile is a first/second/third level connection from you.
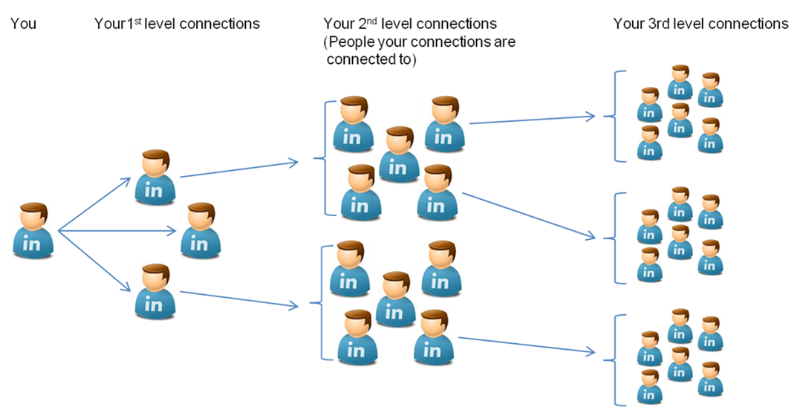
Picture from Linkedin.
One of the most famous (dare I say, THE most famous) Shortest Path Finder Algorithm is Dijkstra’s Algorithm, which is based on three steps:
- Find the cheapest unvisited node reachable
- Mark it as visited and keep track on which nodes you can visit from it
- Repeat
The algorithm ends as soon as we reach the destination node, or whenever there are no more reachable nodes.
When I say cheap I mean the node that costs less to reach from all the nodes we’ve visited so far.
This cost comes from the connections: sometimes the graph connections are equal (like the Facebook friendships, there’s no difference between one connection and another) but sometimes they differ: if you have two ways to go to your home, one way might be easier/cheaper, than the other because on the latter you may have to climb a mountain or something.
Swift Time!
Now that we’re all up to speed, let’s implement everything in Swift!
Node
class Node {
var visited = false
var connections: [Connection] = []
}
The Node class will be nothing more than a property (used by the algorithm) to see if we’ve visited it already, and an array of connections to other nodes.
Connection
class Connection {
public let to: Node
public let weight: Int
public init(to node: Node, weight: Int) {
assert(weight >= 0, "weight has to be equal or greater than zero")
self.to = node
self.weight = weight
}
}
As seen in the Node definition, each connection is assigned to a specific node, therefore all we need to define inside the connection itself is its weight (also known as cost) and the node it connects to.
I’m obviously using the mono-directional connections, this way it’s easier to manage both bidirectional and mono-directional Graphs.
Path
Lastly we need define a path: a path is nothing more than a successions of nodes.
This will help us keeping track which paths in our graph we’ve already visited and how we got there.
More importantly, our algorithm will return us this entity to describe the shortest path between our challenge source node and destination node.
We will use a recursive way for this definition:
class Path {
public let cumulativeWeight: Int
public let node: Node
public let previousPath: Path?
init(to node: Node, via connection: Connection? = nil, previousPath path: Path? = nil) {
if
let previousPath = path,
let viaConnection = connection {
self.cumulativeWeight = viaConnection.weight + previousPath.cumulativeWeight
} else {
self.cumulativeWeight = 0
}
self.node = node
self.previousPath = path
}
}
For convenience, I’m also adding a cumulativeWeight property to keep track on the cost to reach the path’s node: this cost is the sum of all the connections weights that we have traveled from the source node to this node.
The Algorithm
Everything is set! Let’s dig into the algorithm:
func shortestPath(source: Node, destination: Node) -> Path? {
var frontier: [Path] = [] {
didSet { frontier.sort { return $0.cumulativeWeight < $1.cumulativeWeight } } // the frontier has to be always ordered
}
frontier.append(Path(to: source)) // the frontier is made by a path that starts nowhere and ends in the source
while !frontier.isEmpty {
let cheapestPathInFrontier = frontier.removeFirst() // getting the cheapest path available
guard !cheapestPathInFrontier.node.visited else { continue } // making sure we haven't visited the node already
if cheapestPathInFrontier.node === destination {
return cheapestPathInFrontier // found the cheapest path 😎
}
cheapestPathInFrontier.node.visited = true
for connection in cheapestPathInFrontier.node.connections where !connection.to.visited { // adding new paths to our frontier
frontier.append(Path(to: connection.to, via: connection, previousPath: cheapestPathInFrontier))
}
} // end while
return nil // we didn't find a path 😣
}
Yup, just 23 lines of code.
Firstly we define the frontier: the frontier is a collection of paths to nodes that can reach from the nodes the we’ve visited so far.
It’s initially empty, but as soon as we launch the script we will add a path to our start node (line 6).
We can now start following the Dijkstra’s Algorithm steps:
1. Find the cheapest unvisited node
To do so we extract the cheapest path from our frontier (line 9), check if the node was not visited yet and, if it is not, we proceed to the next step (line 10).
2. Mark it as visited and keep track on which nodes you can visit from it
As soon as we reach this step we make sure to mark our node as visited (line 16), and then we add all the new (unvisited) reachable nodes from this node by exploring its connections (lines 18–20).
3. Repeat
The while cycle is now complete, therefore we really just repeat the two steps above!
Note 1
As you may have noticed, we do something between step 1 and 2 (line 12–14): we check if the new cheapest node is our destination node: if it is, congrats! 🎉 We’ve completed the algorithm! Otherwise we continue to step 2.
Note 2
The algorithm may return an optional (line 1 and 22): it is possible that the source and destination nodes don’t have a path that connect each other.
👾 Swift Playground
All right! We’ve now everything we need to play with the Dijkstra algorithm in Swift! Here’s the Playground with an example at the bottom.
class Node {
var visited = false
var connections: [Connection] = []
}
class Connection {
public let to: Node
public let weight: Int
public init(to node: Node, weight: Int) {
assert(weight >= 0, "weight has to be equal or greater than zero")
self.to = node
self.weight = weight
}
}
class Path {
public let cumulativeWeight: Int
public let node: Node
public let previousPath: Path?
init(to node: Node, via connection: Connection? = nil, previousPath path: Path? = nil) {
if
let previousPath = path,
let viaConnection = connection {
self.cumulativeWeight = viaConnection.weight + previousPath.cumulativeWeight
} else {
self.cumulativeWeight = 0
}
self.node = node
self.previousPath = path
}
}
extension Path {
var array: [Node] {
var array: [Node] = [self.node]
var iterativePath = self
while let path = iterativePath.previousPath {
array.append(path.node)
iterativePath = path
}
return array
}
}
func shortestPath(source: Node, destination: Node) -> Path? {
var frontier: [Path] = [] {
didSet { frontier.sort { return $0.cumulativeWeight < $1.cumulativeWeight } } // the frontier has to be always ordered
}
frontier.append(Path(to: source)) // the frontier is made by a path that starts nowhere and ends in the source
while !frontier.isEmpty {
let cheapestPathInFrontier = frontier.removeFirst() // getting the cheapest path available
guard !cheapestPathInFrontier.node.visited else { continue } // making sure we haven't visited the node already
if cheapestPathInFrontier.node === destination {
return cheapestPathInFrontier // found the cheapest path 😎
}
cheapestPathInFrontier.node.visited = true
for connection in cheapestPathInFrontier.node.connections where !connection.to.visited { // adding new paths to our frontier
frontier.append(Path(to: connection.to, via: connection, previousPath: cheapestPathInFrontier))
}
} // end while
return nil // we didn't find a path 😣
}
// **** EXAMPLE BELOW ****
class MyNode: Node {
let name: String
init(name: String) {
self.name = name
super.init()
}
}
let nodeA = MyNode(name: "A")
let nodeB = MyNode(name: "B")
let nodeC = MyNode(name: "C")
let nodeD = MyNode(name: "D")
let nodeE = MyNode(name: "E")
nodeA.connections.append(Connection(to: nodeB, weight: 1))
nodeB.connections.append(Connection(to: nodeC, weight: 3))
nodeC.connections.append(Connection(to: nodeD, weight: 1))
nodeB.connections.append(Connection(to: nodeE, weight: 1))
nodeE.connections.append(Connection(to: nodeC, weight: 1))
let sourceNode = nodeA
let destinationNode = nodeD
var path = shortestPath(source: sourceNode, destination: destinationNode)
if let succession: [String] = path?.array.reversed().flatMap({ $0 as? MyNode}).map({$0.name}) {
print("🏁 Quickest path: \(succession)")
} else {
print("💥 No path between \(sourceNode.name) & \(destinationNode.name)")
}
Conclusion
In the academic world there are discussions on whether Graph Theory should replace Geometry in our schools curriculum: as a Computer Engineer myself, I can see why this might happen in the future 😁.
I hope you’ve learn something new today! Till next time 👋🏻
⚠️️ Note️ ⚠️️ Some readers have pointed out that the
frontierarray is not the most efficient approach to obtain the cheapest available path, because of its sorting overhead. I agree, there are better ways: for example by using Priority Queue data structure. Thanks to u/madiyar and Ilya Myakotin for the support!
 @zntfdr
@zntfdr